Revisiting Zeroth-Order Optimization for Memory-Efficient LLM Fine-Tuning: A Benchmark

Yihua Zhang, Pingzhi Li, Junyuan Hong, Jiaxiang Li, Yimeng Zhang, Wenqing Zheng, Pin-Yu Chen, Jason D. Lee, Wotao Yin, Mingyi Hong, Zhangyang Wang, Sijia Liu, Tianlong Chen

February 2024

Abstract

In the evolving landscape of natural language processing (NLP), fine-tuning pre-trained Large Language Models (LLMs) with first-order (FO) optimizers like SGD and Adam has become standard. Yet, as LLMs grow {in size}, the substantial memory overhead from back-propagation (BP) for FO gradient computation presents a significant challenge. Addressing this issue is crucial, especially for applications like on-device training where memory efficiency is paramount. This paper proposes a shift towards BP-free, zeroth-order (ZO) optimization as a solution for reducing memory costs during LLM fine-tuning, building on the initial concept introduced by MeZO. Unlike traditional ZO-SGD methods, our work expands the exploration to a wider array of ZO optimization techniques, through a comprehensive, first-of-its-kind benchmarking study across five LLM families (Roberta, OPT, LLaMA, Vicuna, Mistral), three task complexities, and five fine-tuning schemes. Our study unveils previously overlooked optimization principles, highlighting the importance of task alignment, the role of the forward gradient method, and the balance between algorithm complexity and fine-tuning performance. We further introduce novel enhancements to ZO optimization, including block-wise descent, hybrid training, and gradient sparsity. Our study offers a promising direction for achieving further memory-efficient LLM fine-tuning. The code is available at the URL.

Type

Preprint

Publication

In Preprint

Zeroth-order (ZO) optimization methods are often preferred for its gradient-free nature which makes it more memory efficient and probably computation efficient. Though first-order (FO) optimization methods are more accurate in gradient computation, it is hard for LLM to fit into a memory-limited devices leading to strong demand for memory-efficient optimization methods. In the benchmark, we empirically get insights into the battle between FO and ZO. Importantly, we answer these questions

When ZO methods have strong memory efficiency compared to all FO methods?
How is the performance of ZO methods compared to the FO methods?
Are ZO methods really faster than FO methods?

Delayed Memory Inefficiency of SGD

Memory peak is the bottleneck for adopting a LLM into a memory-limited device. To find the memory peak, we need to look at the process of optimization which can be unfolded in four steps:

Step 0: Model Loading: Initialize the model with parameter $\mathbf{x}$;
Step 1: Forward Pass: Compute loss $\ell(x)$, and save forward pass states $\mathbf{s}_{\text{fwd}}$;
Step 2: Backward Pass: Calculate gradients w.r.t. $\mathbf{x}$, and generate backward states $\mathbf{s}_{\text{bwd}}$;
Step 3: Optimization Step: Update $\mathbf{x}$ and $\mathbf{s}_{\text{opt}}$ using gradients and utilize temporal state $\mathbf{s}_{\text{opt}}'$ that will be released immediately;

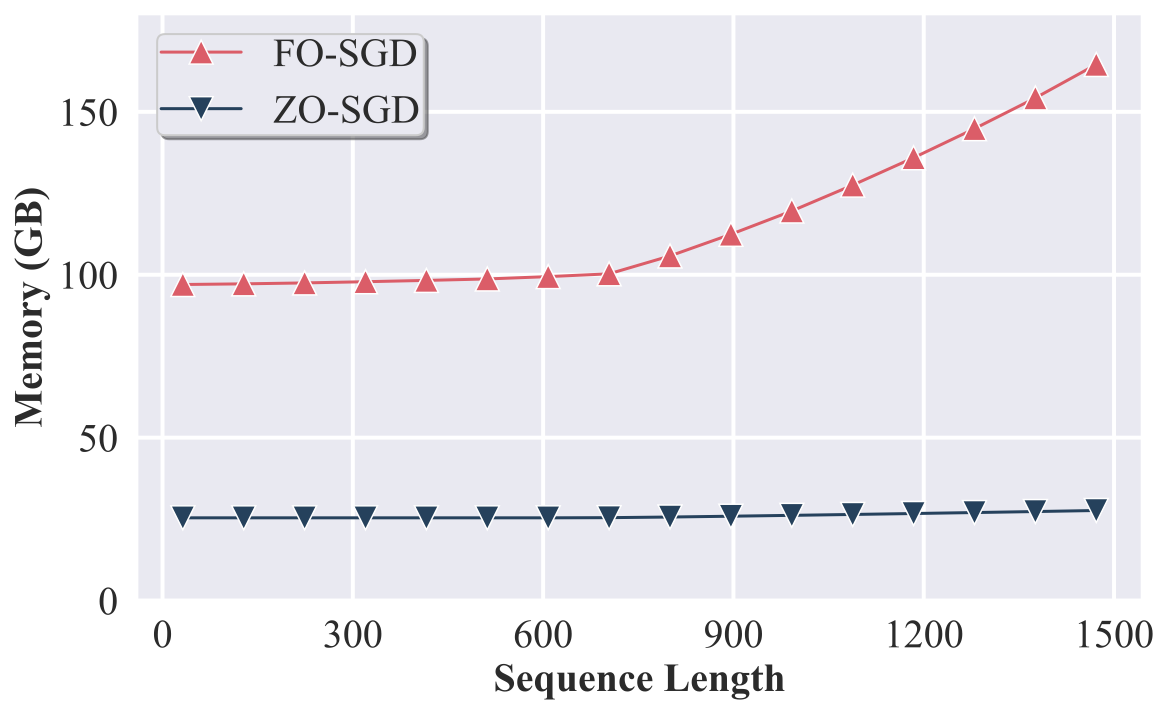
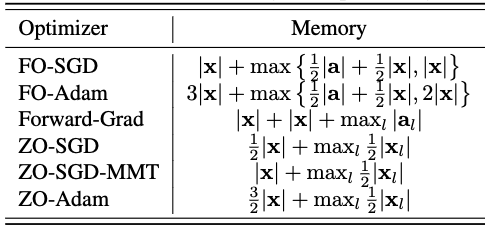
In the below figure, we provide a theoretic analysis based on the general pipeline. A interesting observation is the $\max$ operation in the peak memory estimation because the peak memory is been chosen from the three steps with dynamic memory allocation. For example, FO-SGD consumes $|\mathbf{x}| + \max [ \frac{1}{2}|\mathbf{a}| + \frac{1}{2}|\mathbf{x}|, |\mathbf{x}| ]$. In comparison, ZO-SGD requires $\frac{1}{2} |\mathbf{x}| + \max_l \frac{1}{2} |\mathbf{x}_l|$ memory. The memory efficiency advantage of ZO-SGD will be gradually increased by $\frac{1}{2}|\mathbf{a}|$ if activation memory overwelms the parameters', i.e., $\frac{1}{2}|\mathbf{a}| > \frac{1}{2}|\mathbf{x}|$. That means if the model is not very large and the activation is very dense, then the advantage of ZO methods will be reduced.

Fig: Comparison of total memory complexity of different optimizers when fine-tuning the full model. $|\mathbf{x}|$ denotes the memory of parameters (or gradients in the same size) in full precision. $|\mathbf{a}|$ denotes the memory consumption of intermediate results saved for post-hoc backward during forward. $|\mathbf{x}_l|$ and $|\mathbf{a}_l|$ represents the parameter and intermediate memory of a specific layer $l$.

We empirically demonstrate the advantage delayed memory inefficiency of FO-SGD in the below figure. Obviously, the memory inefficiency of FO-SGD is augmented with long context just like inference.